公開日:

サイトスピード指標の対数正規分布を確かめる

Authors
  • author image
    Name
    代表取締役 宮永邦彦
    Twitter
    @miyanaga

  • 画像軽量化とWebフロントエンドのスピード改善の専門家です。Web系のIT技術大好き。

    このサイトではスピード改善のリアルや、日々の技術的な気づきを共有します。

Core Web Vitals をはじめとするサイトスピード指標の多くは、対数正規分布 に基づくとされている。

実際に Google はその前提に基づき PageSpeed Insights のスコアを設計しており、弊社も「そのようなものだ」としてデータを扱っている。

しかし今一度、その前提を自分の目で確かめてみようと思った。

この記事では、サイトスピードに特化した無料のアクセス解析ツールである Speed is Money で計測したサイトスピード指標が本当に対数正規分布に基づくのか、いくつかの視点から確認をしてみた。

対数正規分布とは ​

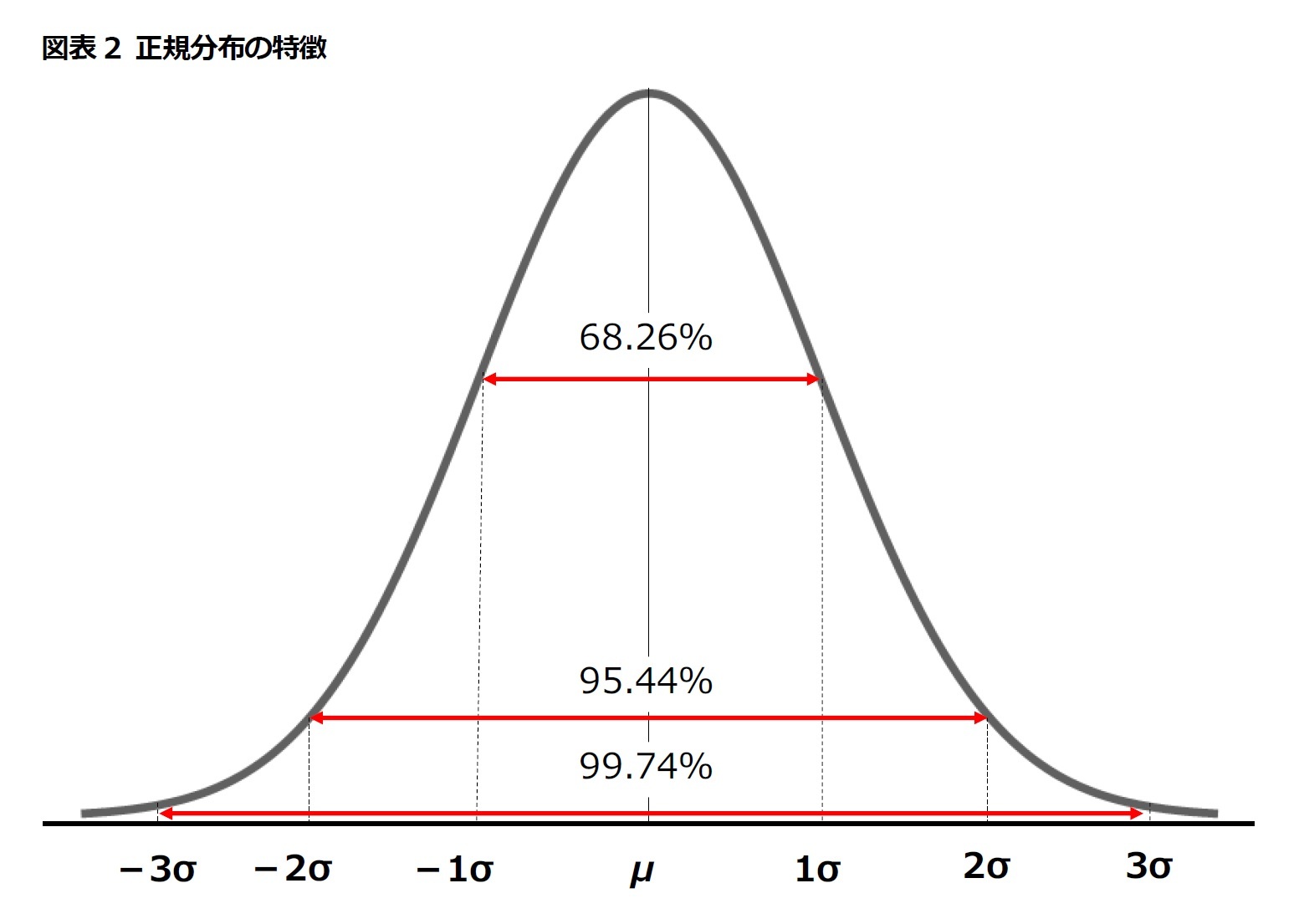
はじめに 対数正規分布 とは何か。「対数」のつかない 正規分布 はよく知られている。平均値を中心とした左右対称の釣鐘型の分布だ。

正規分布

一方、対数正規分布は正規分布にやや似ているが右側がなだらかな坂になっている。正確には正規分布の対数を取ったものが正規分布に従う分布である。

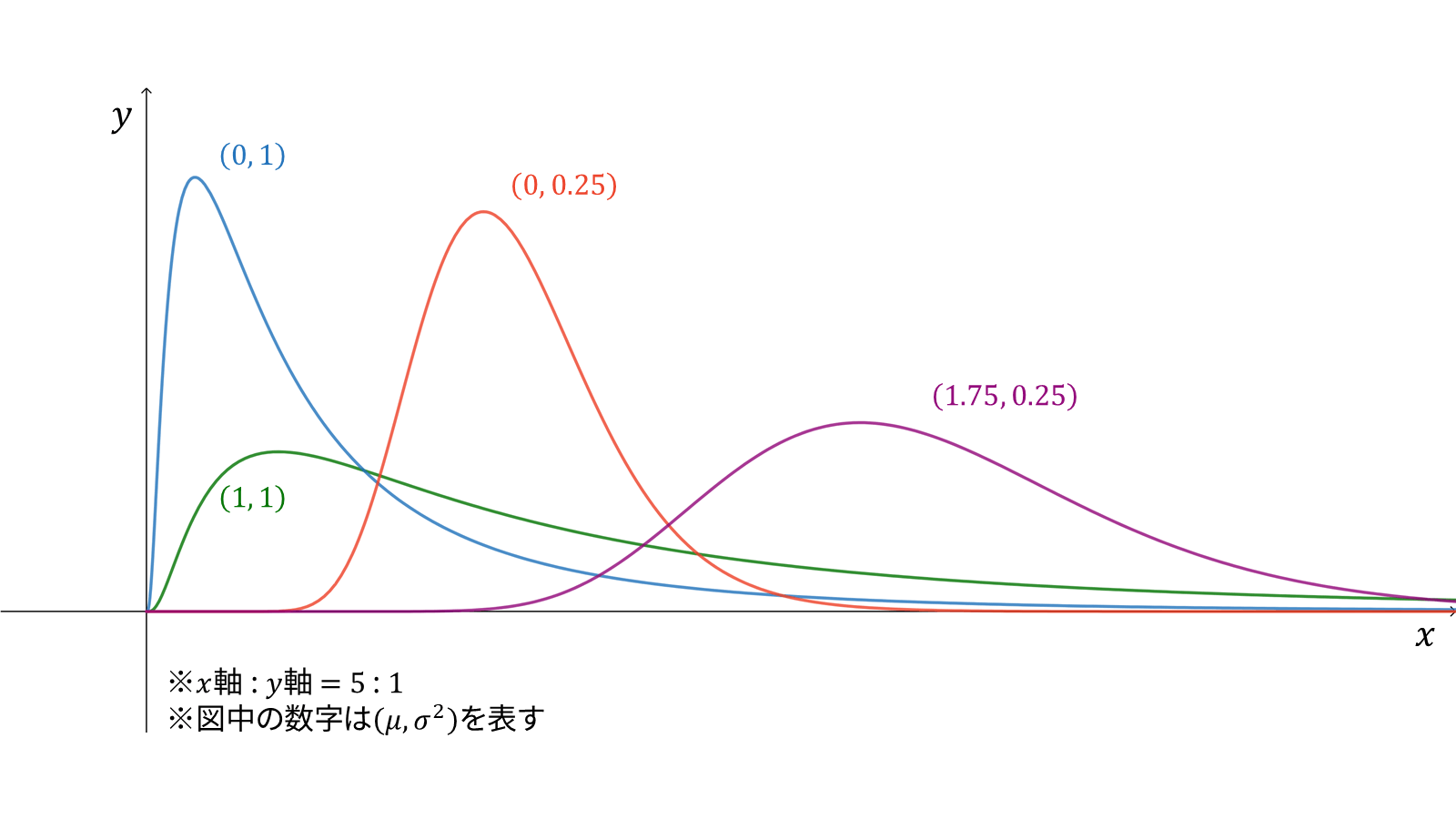
対数正規分布

感覚的には 「正規分布のように一定のボリュームゾーンがあるが、大きい方の値は極端に大きいものまで発散がちになる」 といった理解でよいだろう。

身近な例では身長は正規分布に従い、体重は対数正規分布に従うと言われることがある。例えば成人男性の平均身長を 170cm とすると、2 倍の 340cm という身長はまずありえない。しかし体重は平均 60kg とすると、2 倍の 120kg という体重はあり得るし、もっと大きな体重の人もいる。

ページの読み込み時間(OnLoad)の理論的分布 ​

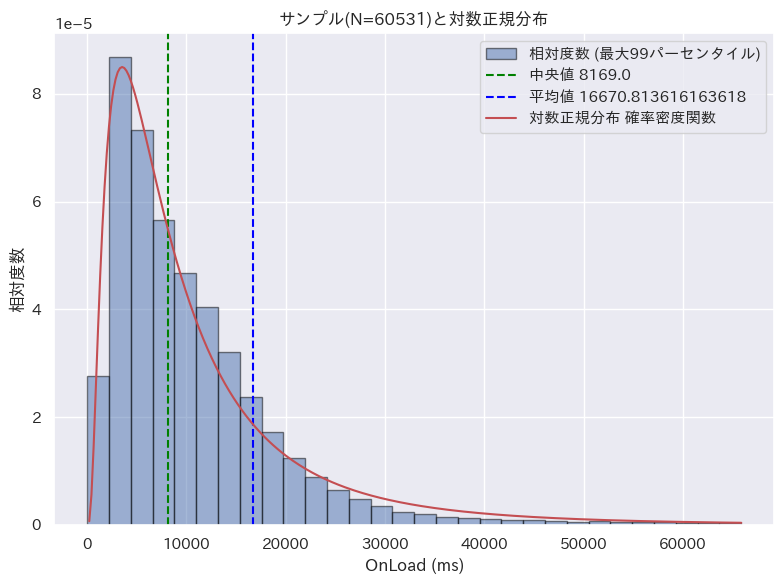
以下はとある通販サイトのページ読み込み時間(Onload)のサンプルから描いたヒストグラムと、理論的に計算された対数正規分布を赤い線で示したものだ。

OnLoadにかかった時間(ms)のヒストグラム、対数正規分布の近似曲線、平均値、中央値

INFO

モバイル端末でのサンプルを抽出している。また、遅いサンプルは極端に遅く、グラフが右に伸びすぎしてしまう。そのためサンプルは 99 パーセンタイルまでで絞り込んでいる。

両グラフの形状は酷似しており、感覚的にはほぼ一致と言えそうだ。

正規分布化 ​

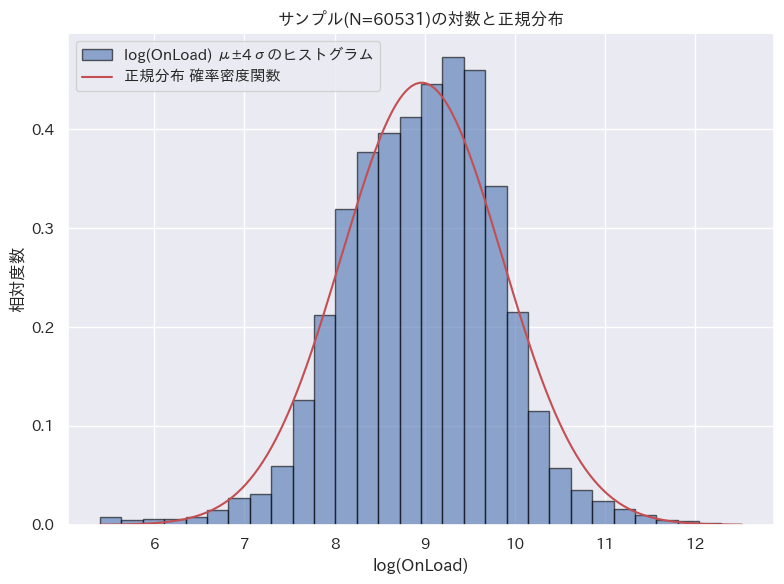
対数正規分布は、X 軸を対数目盛にすると正規分布と同じ形状になる分布 と言い換えることもできる。

上記と同じページ読み込み時間(OnLoad)に対し、自然対数をとったデータのヒストグラムと、理論的な正規分布(赤い線)を重ねたものだ。

サンプル数60531の対数と正規分布

INFO

上記のグラフは平均値が中央に見やすくなるよう、対数を取ったデータの平均値から ±4σ に絞りこんでいる。

右上に多少飛び出しが見られるが、こちらも形状の差異は小さい。

正規分布の検定 ​

サンプルが正規分布に基づくか確率的に検定する方法がいくつかある。それを計算してみた結果が以下だ。

残念ながらいずれの方法でも 「正規分布に基づくとは言えない」 という結果となった。

シャピロ=ウィルク検定
ShapiroResult(statistic=0.9975211655795352, pvalue=1.6639813843026255e-28)
コルモゴロフ=スミルノフ検定
KstestResult(statistic=0.9999999998390625, pvalue=0.0, statistic_location=6.2878585601617845, statistic_sign=-1)
ダゴスティーノの歪度検定
SkewtestResult(statistic=-6.180829491913321, pvalue=6.376565892991275e-10)
ダゴスティーノの尖度検定
KurtosistestResult(statistic=2.199180579201117, pvalue=0.027865084693154626)
オムニバス検定
NormaltestResult(statistic=43.03904842804084, pvalue=4.5101333284193215e-10)

INFO

e-28は、× 10 の-28 乗を示す。つまり非常に小さな値。

p 値 (pvalue)が 0.05 (信頼水準 95%)以下の場合、帰無仮説「正規分布に基づく」を棄却するという判断になるが、いずれの検定結果も p 値が 0.05 に届かず正規分布に基づく仮説は棄却されてしまった。

今回のケースは比較的サンプルが多い(約 6 万点)。サンプルが多すぎるとわずかな違いも大きく反映されやすい、といった言及もあった。筆者の専門性ではこれ以上の追求は難しく、今後の課題のひとつとしたい。

Q-Q プロットによる確認 ​

視覚的な比較方法として Q-Q プロット も試してみる。Q-Q プロットはサンプルと理論的な分布の累積値の差分を示すグラフで、両者が近いほど直線に近づく。

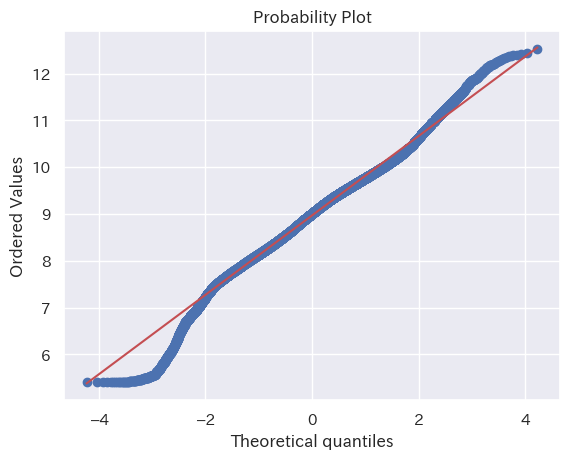
確率プロット図

ほぼ直線で一致に近い、と言っても賛同を多く得られるだろう。

読み込み時間(OnLoad)は対数正規分布に基づく！ ​

以上のように、検定ではスッキリした結果がでなかったが、視覚的には読み込み時間(OnLoad)は対数正規分布に基づくように感じる。

理論的な分布とのフィットには判断は恣意的な余地があり、用途によっては多少精度が粗くてもよいものらしい。

弊社としては、今後も 読み込み時間(OnLoad)は対数正規分布に基づく をポリシーとする。

Core Web Vitals は対数正規分布に基づくか ​

Core Web Vitals の 3 つの指標についても同様の確認をおこなった。それぞれの画像をクリックすると詳細を閲覧できる。

LCP (Largest Contentful Paint)CLS (Cumulative Layout Shift)INP (Input to Next Paint)
対数正規分布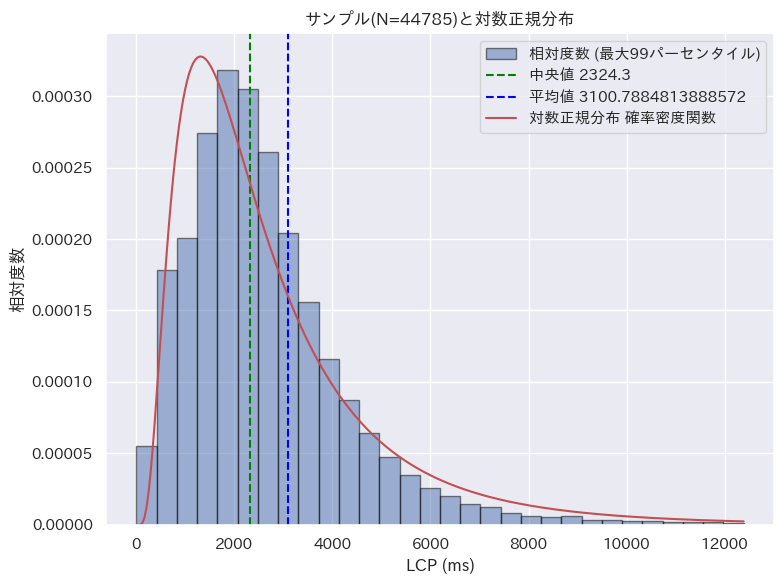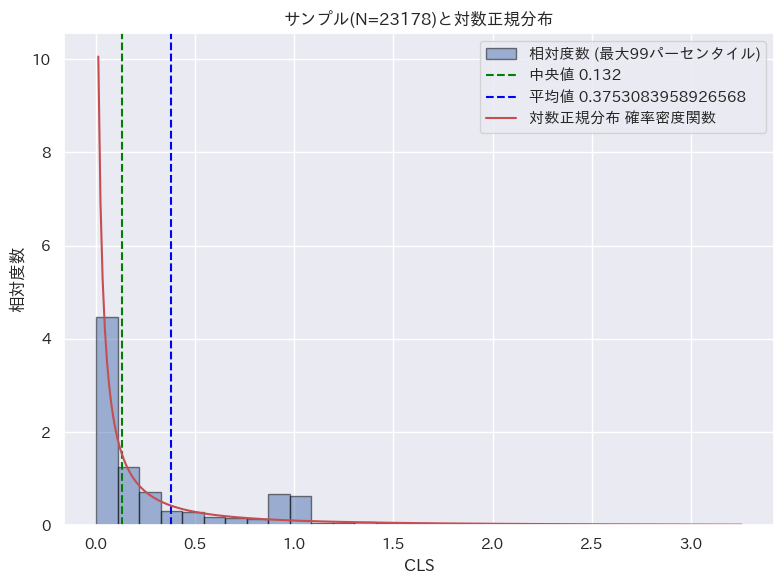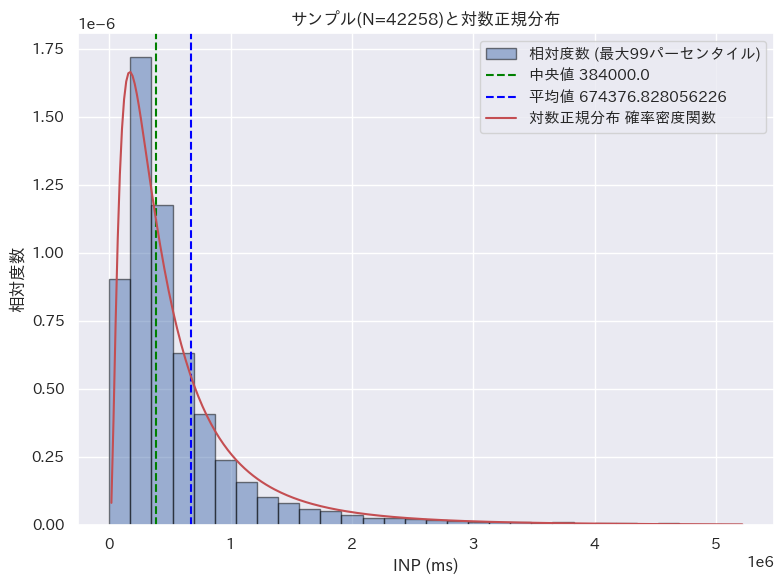サンプル数23178のヒストグラムと対数正規分布の確率密度関数サンプル数42258のヒストグラム。対数正規分布で近似できる。
正規分布サンプル数44785の対数と正規分布log(CLS)のヒストグラムと正規分布サンプル数42258の対数と正規分布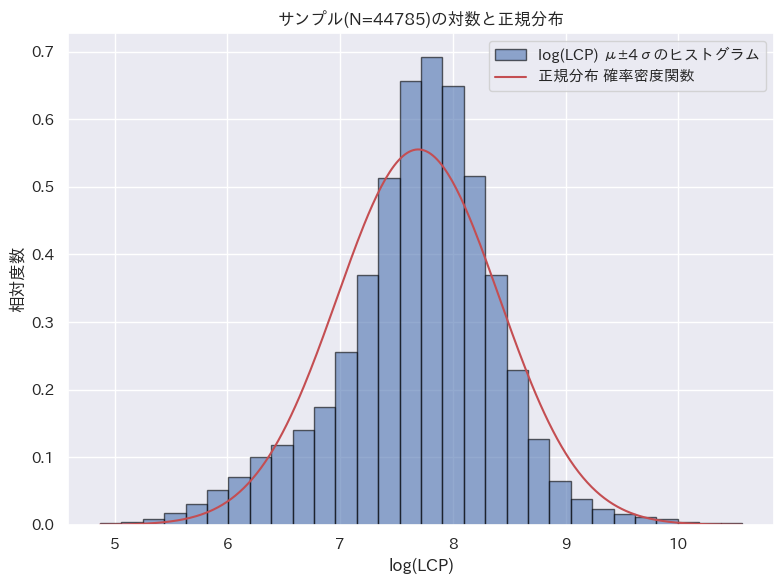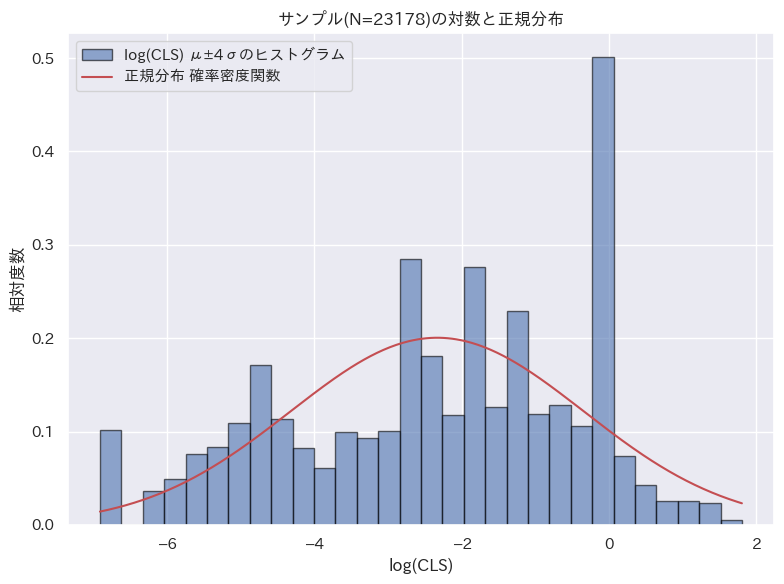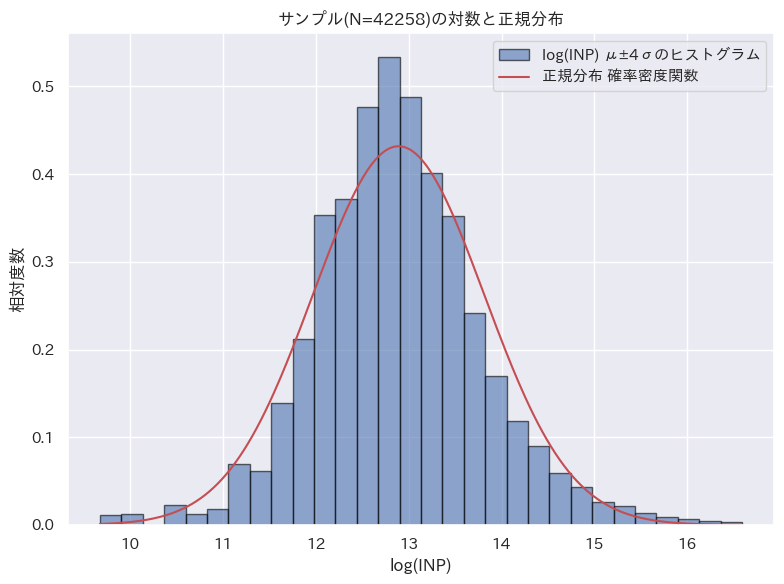
Q-Qプロット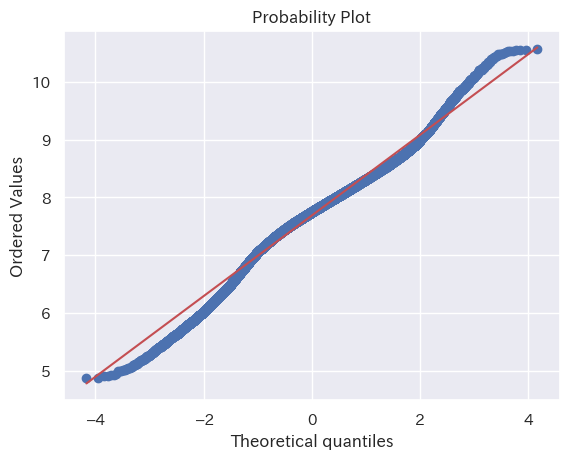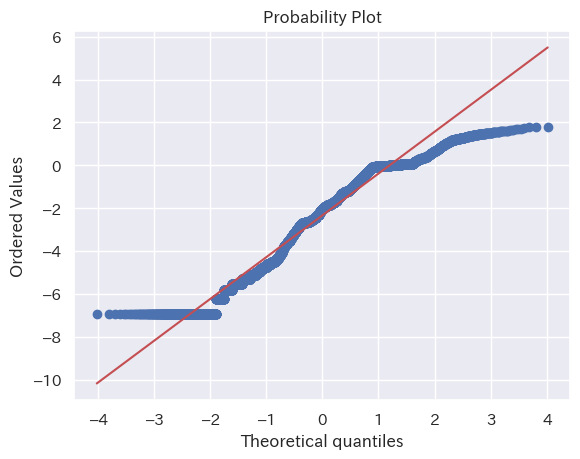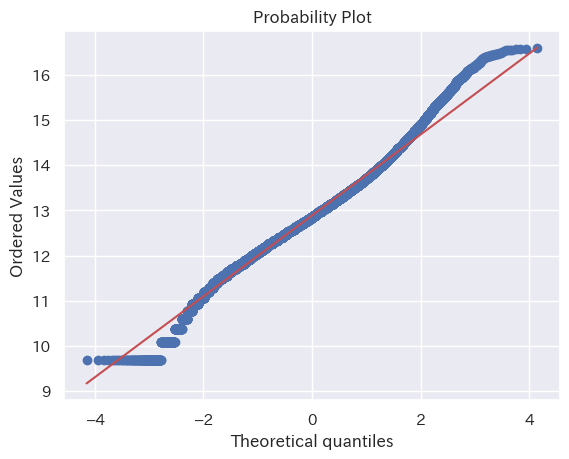確率プロット図確率プロット図確率プロット図

LCP と INP については、対数正規分布に基づくと言えそうだ。CLS についてはやや傾向は見られるが、他の分布に比べると一致度合いは低い。

今回、計測を行ったサイトでは CLS への対応はほぼ万全にできている。従って CLS の値は全体的に小さく、ばらつきも少ない。それが対数正規分布との差異を大きくしたと考えられる。

意外なのは INP である。INP はユーザーの操作に起因する指標であり、その値はユーザーがどのような操作をするかで大きく変わるはずだ。よく行われる操作には偏りがあり、その偏りがもっと個性のように反映されるように思えるが、結局は対数正規分布に近い形状に平準化されている。

まとめ ​

ページの読み込み時間(OnLoad)に加え、Core Web Vitals もほぼ対数正規分布に基づくと言えそうだ。

Google の判断に従い前提としてきたことであったが、改めて自身の実感としても確認できた。データを扱う上で、ときどき常識を疑うのは無駄ではないだろう。

サンプルと理論的な分布のフィットを探る学習にもなったし、Python によるデータ処理やグラフ描画のよい練習にもなった。