- 公開日:
サイトスピードとCVRの関係を数式で記述する - 指数減衰モデル
- Authors
- Name
「読み込みが1秒速くなるとCVRが○%上がる」——サイトスピードとコンバージョンレート(CVR)の関係について、これまで耳にしてきたのはこうした断片的なフレーズばかりだった。しかし、両者の関係をもっと全体的に、シンプルな数式で記述できないだろうか。
14の通販サイトからデータ提供をいただき分析を進めた結果、シンプルな数式でその関係をかなり正確に表現できることが分かった。それが以下の指数減衰モデルである。
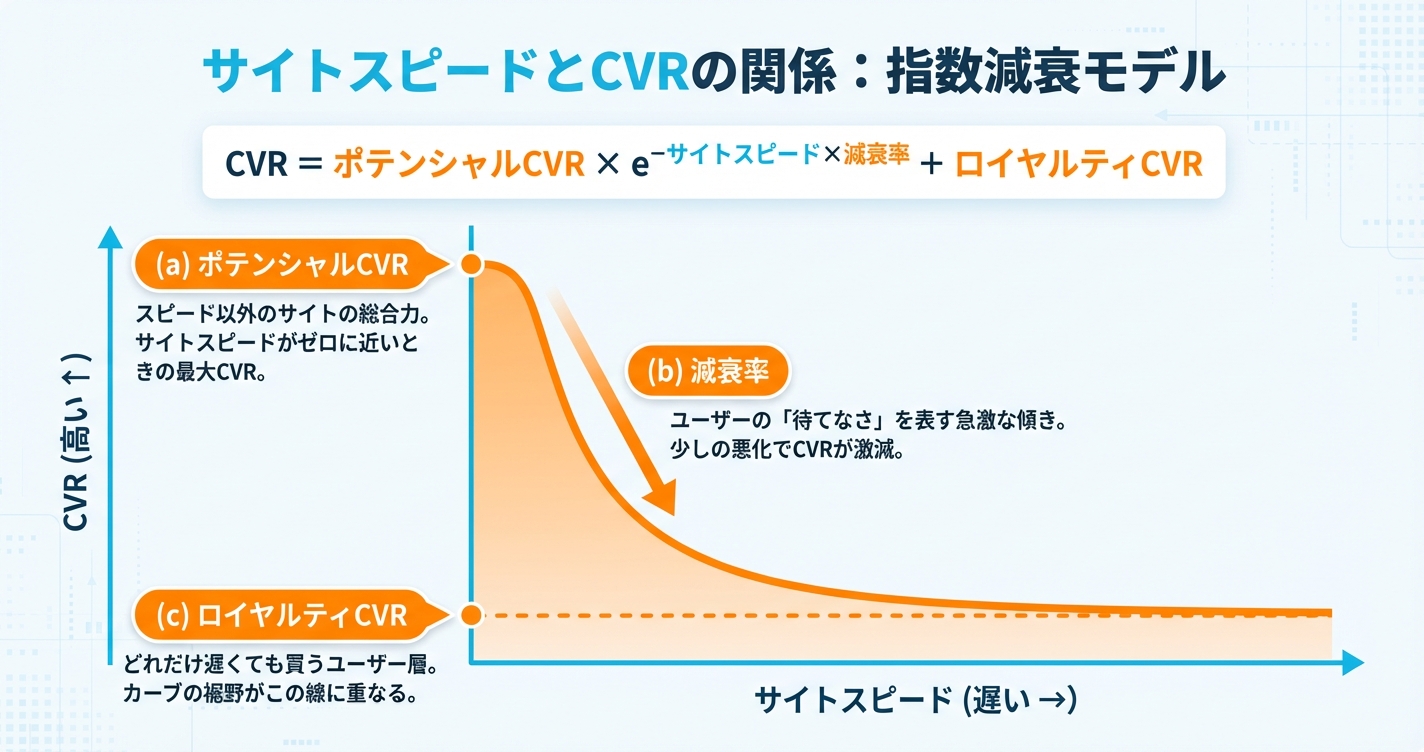
サイトスピードとCVRの関係は「曲線」を描く
まず、サイトスピードの代表的な指標である LCP(Largest Contentful Paint) とCVRの関係をグラフで確認する。
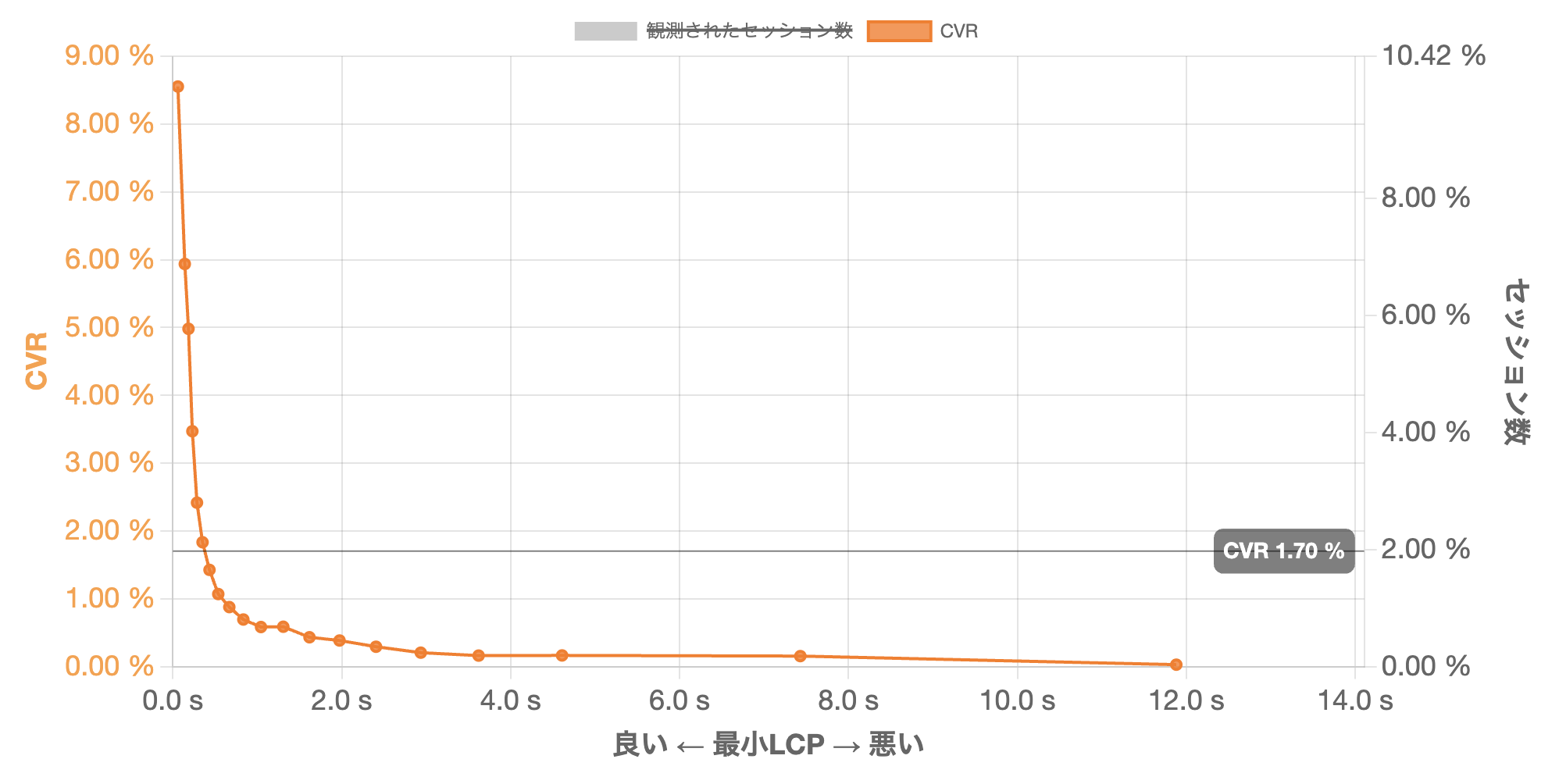
14サイトの集計データから、LCPの値ごとにCVRをプロットしたものである。一目見て分かるように、両者の関係は単純な直線(線形)ではない。
特徴的なのは以下の点だ。
- LCPが良好な最初のわずかな区間でのみ、CVRは非常に高い
- 少しでもLCPが悪化すると、CVRは急激に低下する
- ある程度遅くなると、CVRはほぼ底を打ち、それ以上変化しなくなる
このような「急激に低下して、やがて水平に近づく」カーブを数式で表現するには、どのようなモデルが適切だろうか。
LCPとCVRの関連づけについて
本記事では、ユーザーごとの 最小LCP(そのユーザーが体験した中で最も速かったLCPの値)を横軸に用いている。なぜ平均値や中央値ではなく最小LCPを採用するのか、その理論的背景と妥当性については以下の記事で詳しく解説している。
4つの数学モデルを比較
先ほどの曲線的な減衰パターンを表現できそうな候補として、以下の4つの数学モデルを検討した。
| モデル | 数式 | パラメータ数 |
|---|---|---|
| 対数 | 2 | |
| べき乗 | 2 | |
| 逆数 | 2 | |
| 指数減衰 | 3 |
補正R²について
図中に登場する 補正R² は、モデルが実際の観測値をどれだけ正確に表現できているかを示す指標である。0から1の間の値を取り、1に近いほどモデルの精度が高い。「補正」とはパラメータ数の違いを考慮した補正で、パラメータが多いモデルほどフィッティングしやすい分のペナルティが加えられている。
実際にあるサイトのデータにそれぞれのモデルをフィッティングした結果が以下の図だ。
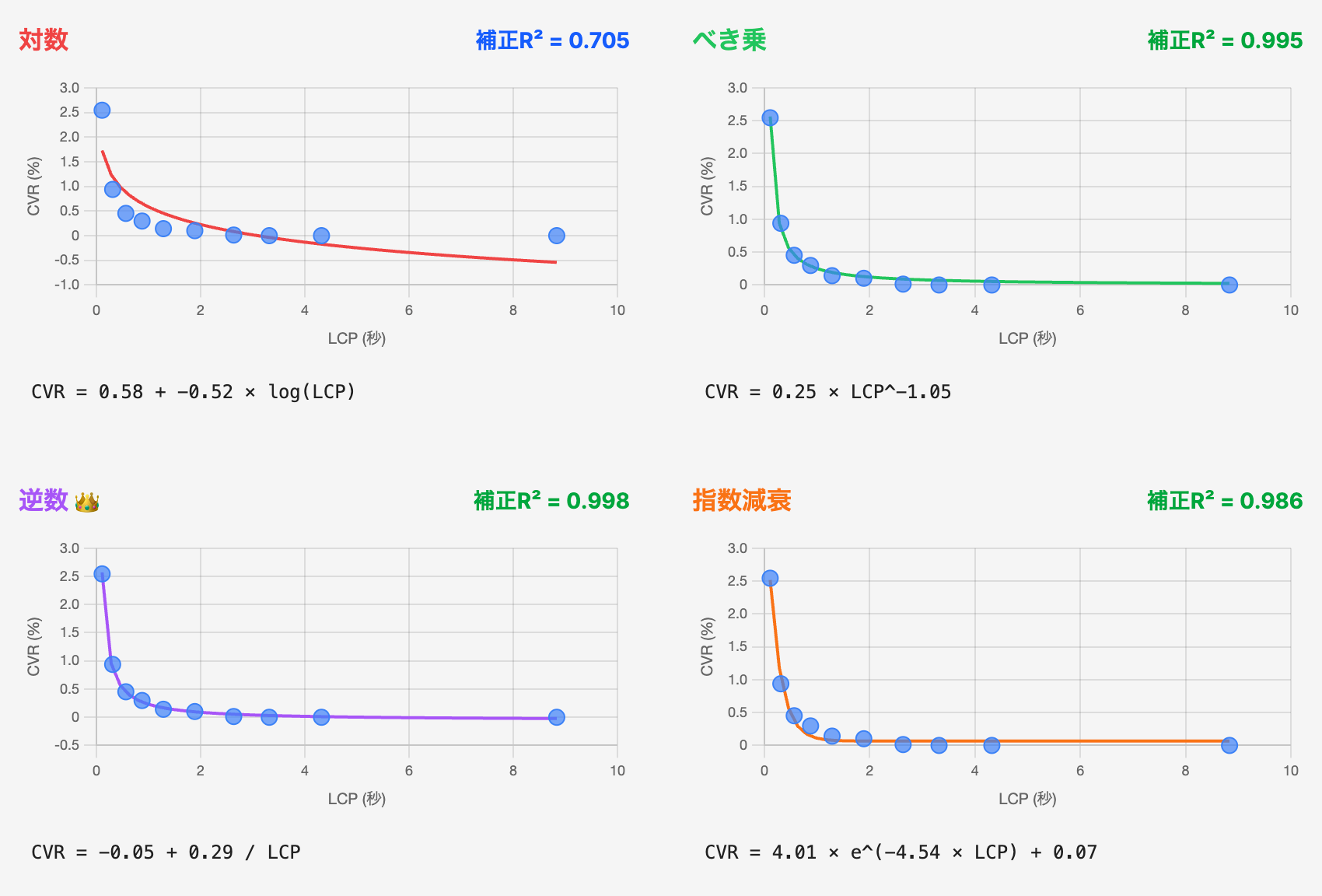
対数モデルはあまりフィットしていないが、べき乗・逆数・指数減衰の3つは実測値の特徴をかなりよく捉えている。特に逆数モデルは補正R²が0.998と、この1サイトにおいては最も高い正確さを示した。
では逆数モデルが最適なのだろうか。1サイトだけの結果で判断するのは早計だ。14サイトすべてについて、モデルの正確さを示す補正R²を比較してみる。
14サイトの補正R²を比較する
14サイトそれぞれについて4つのモデルの補正R²を算出し、箱ひげ図(ボックスプロット)で比較したのが以下の図である。

先ほどの1サイトの例では逆数モデルが最も高い補正R²を示していたが、14サイト全体で見比べると様相が異なる。
- 対数モデル: R²が低く(中央値0.6程度)、ばらつきも大きい。明らかに不適切
- べき乗モデル: 全体的にR²が高いが、ややばらつきがある
- 逆数モデル: べき乗と同程度に高いが、下方向に外れ値がある
- 指数減衰モデル: 圧倒的にR²が高く、かつばらつきが極めて小さい
14サイトを横断して比較すると、指数減衰モデルが最も安定して実測値をよく表現していることが分かった。ほぼすべてのサイトで補正R²が1に近い値を示しており、精度と安定性の両面で他のモデルを圧倒している。
14サイトの指数減衰フィッティング
実際に14サイトそれぞれのデータに指数減衰モデルを当てはめた結果が以下の図である。丸い点が観測値、線が理論値を表している。縦に長い図ではあるが、ぜひざっと目を通してほしい。
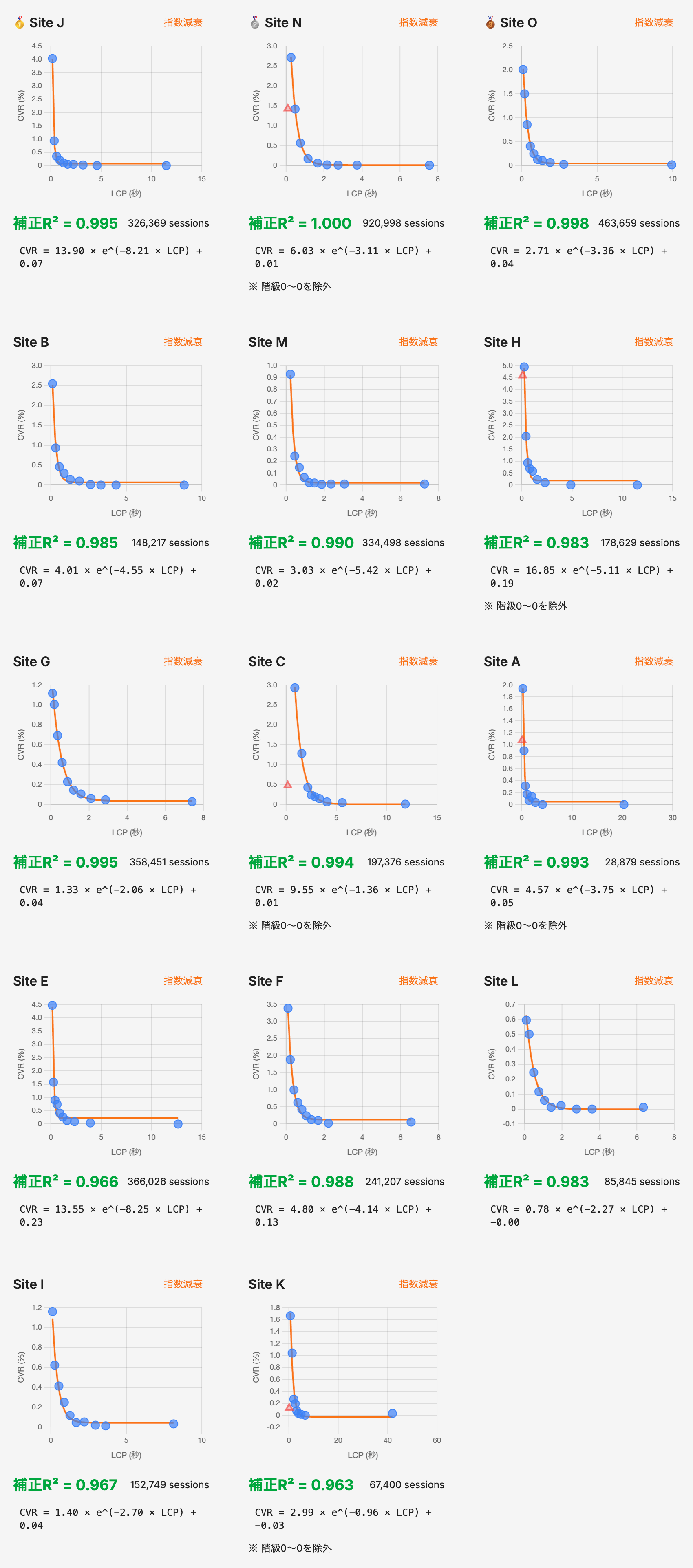
ほぼすべてのサイトにおいて、観測値の点と理論値の線がよく一致していることが見て取れるはずだ。サイトによってCVRの絶対値や減衰のスピードは異なるが、指数減衰という同じ構造がすべてのサイトに共通して現れている。
この分析結果をもって、LCPとCVRの関係性には指数減衰モデルを適用することとしたい。
指数減衰モデルのパラメータが意味するもの
CVRを Y、サイトスピード(LCP等)を x としたとき、指数減衰モデルは3つのパラメータを持つ以下の数式で表される。
それぞれのパラメータが何を意味しているのかを見ていく。
順番は前後するが、まず分かりやすい c から説明する。
c: ロイヤルティCVR
c はサイトがどれだけ遅くても購入してくれるユーザー層によるCVR——いわば ベースラインのCVR を表す。これを ロイヤルティCVR と呼ぶ。
どんなにサイトが遅くても「この商品がどうしても欲しい」「このショップでしか買えない」と思ってくれる忠誠度の高い顧客層は一定数存在する。c はそうした顧客によるコンバージョンの底値であり、商品力やブランドへのロイヤルティの強さが反映されている。
a: ポテンシャルCVR
もしすべてのユーザーが待ち時間によるストレスゼロの体験ができたとしたら、ロイヤルティCVRに対してどれくらいのCVRを上乗せできるだろうか。
a はその 上乗せ分のCVR を表している。これを ポテンシャルCVR と呼ぶことにする。
つまり、スピードの摩擦がゼロのときに達成できる理想のCVRは a + c となる。商品の魅力、ブランドへの信頼、サイトの使いやすさ、顧客の期待度——これらスピード以外のサイトの総合力が a + c に集約されている。
b: 減衰率(CVR半減期の決定因子)
b はCVRがどれだけ速く減衰するかを決めるパラメータであり、ユーザーの「待てなさ」 を示している。
直感的には理解しにくいが、b は CVRの半減期 を決めるパラメータであると解釈すると分かりやすいだろう。
半減期とは文字通り、ポテンシャルCVRが半分に低下するまでのLCPの増加量(秒数)である。たとえば半減期が0.2秒であれば、LCPが0.2秒悪化するだけでCVRが半分になるということだ。
b が大きいサイトは、スピードが少しでも遅くなるとすぐにユーザーが離脱してしまう特性を持っている。逆に b が小さいサイトは、多少遅くても欲しいと思わせる商品やブランドの魅力があるか、あるいはセールや限定キャンペーンなど販促がうまく機能しているケースも考えられる。
これらを日本語で表現すると、冒頭に挙げた以下の数式になる。
LCP以外の指標への適用
LCP以外のスピード指標についても同様の分析を行った。
INP(Interaction to Next Paint)とCVR
INPはLCPと同じくCore Web Vitalsの一角であり、ユーザーのクリックやタップなどの入力に対する応答の速さを示す指標である。

INPに対しても指数減衰モデルは高いフィット精度を示しているが、べき乗モデルのほうがさらに精度が高いという結果になった。
これはINPとCVRの関係が、LCPとCVRの関係よりもかなりシビアな特性を持っているためだ。INPが少しでも悪化するとCVRは瞬間的に低下する。このような急激なカーブを表現するには、指数関数よりもべき乗モデルのほうが適している。
OnLoad(読み込み時間)とCVR

OnLoadに対してはLCPと同様に、指数減衰モデルが圧倒的にフィット精度が高い結果となった。べき乗・逆数モデルよりも明確に優位である。
ページの読み込み完了までの時間であるOnLoadは、LCPと類似した特性を持っており、指数減衰モデルによる記述が適していると言える。
スピードの影響を排除した「サイトの魅力」が見える
改めて、日本語による数式を確認する。
これまでCVRには、スピードの影響とサイト本来の魅力が混在して現れていた。この数式はサイトスピードとCVRの関係性を記述するものであるが、裏を返すと、各パラメータはスピードの影響を取り除いた上での サイト固有の魅力を表す指標 にもなっている。
- ポテンシャルCVRが高い → 商品力、ブランドへの期待、サイトの使いやすさなど、サイトの総合的な魅力が大きい
- 減衰率が小さい → ユーザーが多少の遅さを我慢してでも利用したいと思える、販促や訴求の力が強い。セールや限定キャンペーンなど「今買いたい」と思わせる施策が効いているとも解釈できる
- ロイヤルティCVRが高い → どんなに遅くても買いたいと思わせる、ブランドや商品への忠誠が厚い
つまりこの数式は、サイトスピードの改善に役立てる一方で、それぞれのパラメータの変化がスピード以外のサイトの魅力の増減を表現する指標としても活用できる可能性が大いにある。
本調査の限界と今後
今回の分析はあくまで14サイトのデータに基づくものである。これをもってして「指数減衰モデルがサイトスピードとCVRの関係を普遍的に記述できる」と断言するのは時期尚早だろう。
しかし、調査対象の範囲においては非常に高い精度でフィットし、かつパラメータの意味も直感的で理にかなった数式モデルを発見できたと思う。
次のステップとして考えているのは、サイトスピードの確率分布(対数正規分布に従うことが知られている)と、今回のスピード-CVR関係モデルを合成することだ。通販サイトのスピードと収益性の関係を統合的に記述し、より正確な予測に役立てるモデルを構築する土台が整ったと感じている。